type
status
date
summary
tags
category
icon
password
featured
freq
difficulty
给定两个整数数组
preorder 和 inorder,其中preorder是二叉树的先序遍历,inorder 是同一棵树的中序遍历.构造出二叉树并返回其根节点。
示例 1:
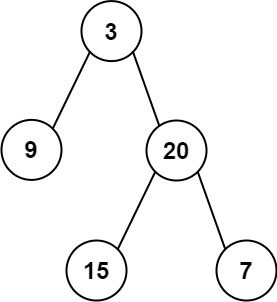
示例 2:
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
3000 <= preorder[i], inorder[i] <= 3000
preorder和inorder均 无重复 元素
inorder均出现在preorder
preorder保证 为二叉树的前序遍历序列
inorder保证 为二叉树的中序遍历序列
解法一:分治 + 哈希表 + 区间索引(推荐)
把前序的根,放回中序的正确位置,然后左右两边继续同样的操作。
前序的第一个一定是整棵树的根;在中序里找到这个根,就把中序分割成“左子树的一段 + 根 + 右子树的一段”。左边那段有多少个节点,前序里紧接着就有多少个属于左子树,其余属于右子树。

为了快,我们用一个哈希表把 中序的值→下标 存起来,这样“找根位置”是 O(1)。再配合“只传左右边界,不切片”,就可以实现 O(N) 时间,空间也只用到哈希表和递归栈。
复杂度
- 时间:O(N)。每个节点只进出一次,哈希表查找 O(1)。
- 空间:O(N)。哈希表 O(N);最坏链状树时递归栈 O(N)。
解法二:分治
每次前序拿一个根,去中序分割出左右两段,然后把左右子树对应的前序/中序传下去。
复杂度
- 时间:最坏 O(N^2)(
index每次 O(N))。如果预先构建中序哈希表,可降到 O(N),但切片拷贝仍有额外常数开销。
- 空间:平均大于 O(N)(频繁切片产生新列表),递归栈最坏 O(N)。
解法三:迭代(栈)
前序是“根、左、右”,中序是“左、根、右”。
我们可以这样想:沿着前序一路建“左链”(不断把新根接到左边),直到中序提示“该回头了”。
当栈顶的节点值正好等于当前中序指针所指的值,说明“这个节点的左子树已经完结”,我们就弹栈并右转。
换句话说:
- 栈里放的是尚未接完右子树的节点;
- 当前序新节点值与中序不等时:它一定是左孩子(继续压栈);
- 一旦相等了:不停弹栈,直到不等为止;弹出的最后一个,就是要接右孩子的位置,然后把新节点挂在它的右边。
这个过程严格遵循两个序列的相对顺序,不需要递归,非常高效。
复杂度
- 时间:O(N)。每个节点最多入栈一次、出栈一次;指针线性扫描。
- 空间:O(N)。栈在退化链情况下可达 O(N)。
解法四:分治 + 生成器
解法一里我们用
pre_i 做“前序游标”。在 Python 里也可以把 preorder 变成一个迭代器(或生成器),每次 next() 一个根,这样就不需要显式维护“当前前序下标”。其余逻辑和“哈希表 + 区间”完全一致。
复杂度
- 时间:O(N)。
- 空间:O(N)(哈希表 + 递归栈)。
- 作者:Fan Luo
- 链接:https://fanluo.me/article/leetcode-105-从前序与中序遍历序列构造二叉树
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
上一篇
[Leetcode 101] 对称二叉树
下一篇
[Leetcode 116] 填充每个节点的下一个右侧节点指针
