type
status
date
summary
tags
category
icon
password
featured
freq
difficulty
写一个高效的算法来搜索
m x n 的 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:
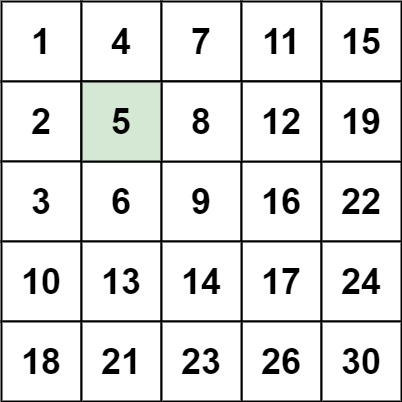
示例 2:
解法一:“Z 字形”扫描(推荐)
矩阵按行、按列都递增。要是有个位置,能一眼判断“往上会变小,往右会变大”,那每次就能排除一整行或一整列。
选右上角或左下角作为起点(这两个点的“局部单调方向”刚好一小一大):
- 以右上角为例
x = 0, y = n-1:
若
matrix[x][y] > target,往左走(整列右侧都更大,直接排除一列);若
< target,往下走(整行上侧都更小,直接排除一行);若相等就返回。
- 这样每步至少扔掉一行或一列,最多走
m+n步。
复杂度
- 时间
O(m+n)
- 空间
O(1)。
解法二:二分搜索+ 轻量剪枝
既然每行有序,直觉上“在可能的行上做二分”就行;
而且还能用端点和
target 比一下,不在范围的行直接跳过。- 先扫每一行
row,只要满足row[0] <= target <= row[-1]才二分。
- 行内用标准二分找
target。
也可以按列来做。 想拿到具体坐标位置,也可以。
复杂度
- 时间:最坏
O(m log n)(m 行,每行一次二分),
- 空间:
O(1)。
解法三:分治
把矩阵看成“有序的 2D 空间”。
拿中点切成四块,用中点与目标的关系去排除不可能的象限,在剩下的两块里递归。
具体步骤:
- 取子矩形左上
(r1,c1)、右下(r2,c2),中点(rm, cm);
- 若
matrix[rm][cm] == target直接命中;
- 若
< target,可以排除左上与上左区域,仅在右上与左下递归;
- 若
> target,反之亦然。
- 递归到越界/空区间就停。
复杂度
- 时间:均摊视数据分布而定;上界可到接近
O(m log n)/O(n log m),
- 空间: 递归栈深度
O(log(m+n))(均衡时)。
- 作者:Fan Luo
- 链接:https://fanluo.me/article/leetcode-240-搜索二维矩阵-ii
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
上一篇
[Leetcode 239] 滑动窗口最大值
下一篇
Demystifying Agentic Search Engines
